Lesson 45: Radial Collision Detector

The hittest() function used in previous games is adequate for rectangular objects. However, it is not as good with all objects.

Consider the following two images. Are they hitting one another?

Using the hittest() from previous lessons, they are hitting each other.

Wouldn't it be wonderful if there was a hittest() that would work well for circular objects?

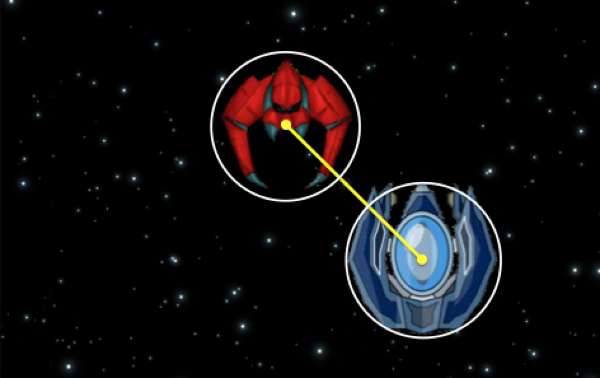
Well, you can do this... with a little math. First, you need to know the distance between the midpoints of the circles.

Derived from the pythagorean theorem, you can use the distance formula to compute this distance. See, algebra does have a purpose.

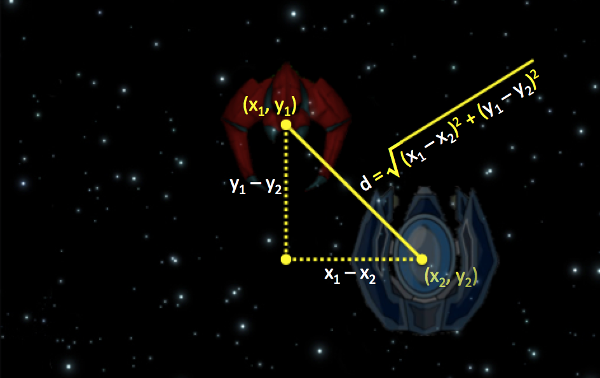
You will also need to know the radius of both circles. If the distance between the midpoints (calculated above) is less than the sum of the radii, then the objects are hitting!

1. Create a hittest() function that checks whether two elements are hitting each other.

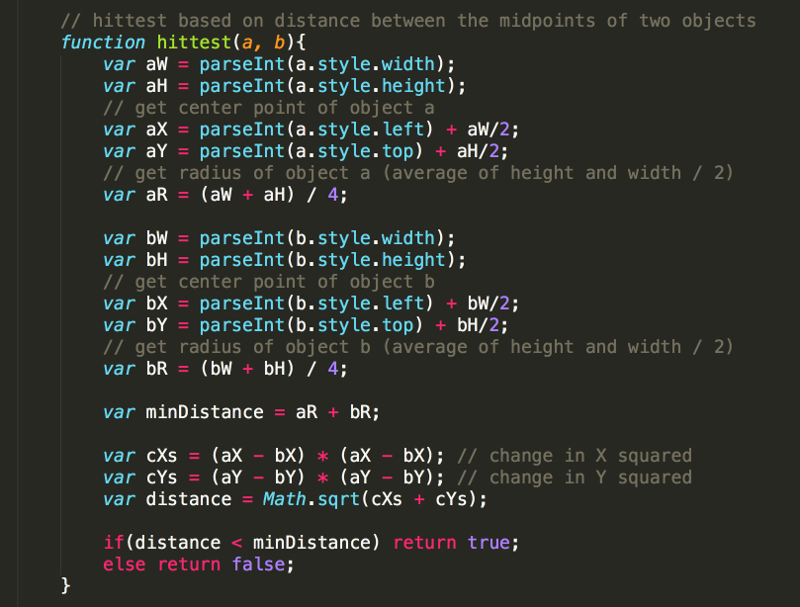
For some, this will bring back nightmares of high school mathematics classes. Do not worry... once the function is written, you only need to understand how to use it (which is exactly the same way we used the previous hittest function), not how it works.

Still, it is worthwhile to take some time to try to understand the math and logic that makes this function work before moving on.

The width and height are determined as usual using the parseInt() function with the elements width and height properties.

The X value of each element's midpoint is calculated using the parseInt() function with the elements left property, and then adding half of the elements width.

Similarly, the Y value of each element's midpoint is calculated using the parseInt() function with the elements top property, and then adding half of the elements hieght.

You know that the images used (and the img element itself) is rectangular, even though the transparent portions of the image make it look more circular. So, how do you get the radius of an element that is actually not a circle? In fact, you should calculate the radius of the inscribed circle.

The diameter of the inscribed circle would be the same as the width, so the radius of the inscribed circle would be half the width.

So, calculating the radius of the element is simple if the width and height of the element were the same. You could just divide this value by 2.

However, if the width and height are not the same, resulting in a rectangle instead of a square and an inscribed oval instead of a circe, which value should you use?

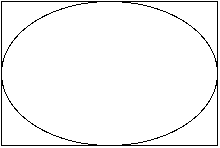
Technically, an oval does not have a radius. However, you get an estimate of the distance from the center to the edge of the oval and use this for the radius.

Take for instance an element that has a width of 120 and a height of 80. Dividing the width by 2 would give you a radius of 60, which is the longest distance from the center to the edge of the oval. Dividing the height by 2 would give you a radius of 40, which is the smallest distance from the center to the edge of the oval. A compromise would be to take the average of the width and height (add 80 and 120 and then divide by 2) to get 100, and then divide that value by 2 to get 50 (which is halway between the smallest distance of 40 and the longest distance of 60).

So to estimate a radius you could use:
r = (w + h) / 2 / 2;, or simplified as:
r = (w + h) / 4;

In fact, the lines:
var aR = (aW + aH) / 4;
var bR = (bW + bH) / 4;
do exactly this to calculate the radius of element a (aR) and the radius of element b (bR).

Recall that the sum of the radii of the two elements is the minimum distance the elements can be apart without colliding. This minimum is calculated in the above code with:
var minDistance = aR + bR;

Then there is the actual distance between the objects (the distance between the midpoints). This is done with the distance formula.

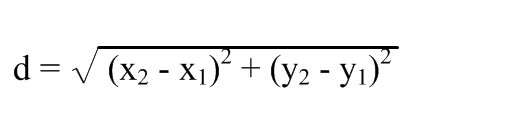
To break the calculation in parts is calculated.
var cx2 = (aX - bX) * (aX - bX);
where cx2 is the change in x squared

Then 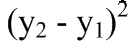is calculated.
var cy2 = (aY - bY) * (aY - bY);
where cy2 is the change in y squared

To finish up, you just add the two values together and take the square root.
var distance = Math.sqrt(cx2 + cy2);

Finally, the appropriate value (true or false) should be returned depending on whether the objects are colliding or not.

2. In the gameloop() function, in the same for loop that you are using to move the enemies, add code to detect when any of the enemies hit the player's ship.

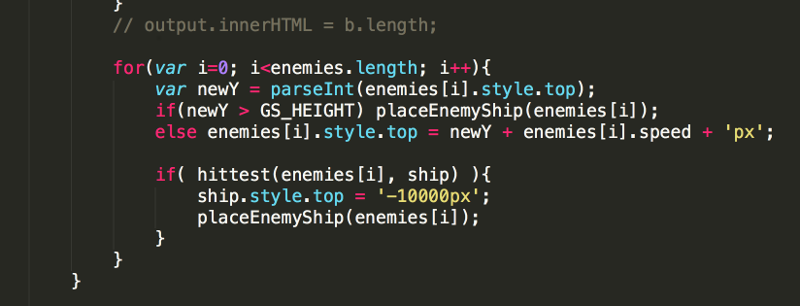
In this case, when a collision occurs the enemy ship is moved above the gameScreen using the placeEnemyShip()function, and the player's ship is placed far off the screen (above all enemy ships) so that no intentional collisions occur. By moving the ships out of view, and ensuring no additional collisions occur, the enemies can continue flying after the game is over, which is sometimes a nice effect.

Of course, you would expect an explosion of some sort instead of the images just dissappearing. You will tackle this in the next lesson.